Writing a priority queue in C# (part 1)
published: Thu, 22-Jan-2004 | updated: Sat, 6-Aug-2016
Just recently I was talking to someone who wanted an implementation of a priority queue written in C#. He'd taken the Delphi source code from my book (shameless plug) and had ported it over. Kudos to him for doing the exercise, but I can't help thinking that it was the wrong thing to do.
Why? Because the priority queue I'd written assumed certain things about the environment to which it was targeted. The .NET Framework is, in some ways, very different from Delphi's VCL. So, really, instead of porting the code, we should step back and re-implement it to target the .NET Framework.
First things first: a quick definition. A priority queue is s data container with two main operations: enqueue and dequeue. Enqueue accepts an item that has an associated priority and adds it to the priority queue. Dequeue removes and returns the item that has the highest priority. Sometimes these operations are known as Push and Pop respectively.
That's all there is to the definition of a basic priority queue. Enhanced versions enable you to dequeue the item with the smallest priority rather than the largest, others enable you to retrieve either the largest or the smallest, others give you the ability to change the priority of items already in the queue, or to remove them completely. However, in this article, we'll just deal with the basic variety.
The simplest efficient algorithm for implementing a priority queue is the heap algorithm, and this is the one I'll use here. (Others include binomial heaps and Fibonacci heaps, as well as other more esoteric varieties.)
A heap, at least in regard to this algorithm, is a balanced binary tree with a special property known as the heap property. A balanced binary tree is a binary tree where every level is complete (no holes), except perhaps the bottommost level. This level, it is not complete, will have all its nodes over as far to the left as possible.
The heap property states that every node in the tree, providing that it is not a leaf node, contains an item that is greater in priority than the items in both its children (or, than its left child, if it has only one). If you think about it for a moment, by recursion, this means any node has a priority that will be greater than its children, its grandchildren, its great-grandchildren, etc. It also means that the item with the highest priority will be found at the root of the tree (handy that!).
What the heap property does not say is that the binary tree is in complete sorted order. It's a looser definition than that. Here's a very small heap:
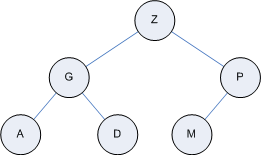
You can see that Z node is greater than any other node (if we take the priority to be the ordinal value of the character). G is greater than its two children, and P is greater than its only child. All the levels are complete apart from the bottommost, and all those nodes are to the left.
Now, before going any further, you should notice something interesting. If we count the Z node as node 0, and count the others level by level going down and from left to right, we get Z as 0, G as 1, P 2, A 3, D 4, and M 5. Notice that there are no gaps. This method of enumerating the nodes is much like an array. In fact, the two representations are isomorphic (equivalent, if you like) and we can implement a heap as an array, rather than a bunch of isolated nodes. So, that's what we'll do. (Notice, by the way, that the node with the highest priority is at item 0 of the array.)
In the operations we'll be discussing in a moment, we shall need to know the parent of a node (if it has one), and the children of a node (if it has any). With the tree representation, this was easy: you followed the relevant links. With an array representation, it's a little obscure. Look at the numbers, though. The parent of node 1 is 0, of node 2 is 0, of node 3 is 1, of node 4 is 2, etc. See the pattern? Subtract 1 from the node number and integer divide by 2. Similarly we can get the children node numbers: double the node number, add 1 or add 2.
With that said, let's look at enqueuing a new item. The basic process is this: add the item to the end of the array (in the tree that's equivalent to adding it at the first empty node in the bottommost layer). Now, the problem with this is that, although we are ensuring the completeness of the heap, we're probably violating the heap property. We should rectify that immediately.
To do so, we use an operation called bubble up. Look at the parent of this new node. Is it's priority less than ours? If so, swap the nodes over (or, rather, swap the items within the nodes). Our new item will have moved up the tree one level. Looking at the heap property from this new vantage point (and ignoring the rest of the tree) we can see that it is greater than both its children. The first child because we just swapped with it because it was smaller, and the second child because it was already smaller than the item we swapped with.
Now we repeat this test-and-swap operation with our new parent, and then, if needed, with the new parent after that, etc. As you can visualize, we are bubbling the new item up the tree until it reaches a point where it's less than its new parent (or it's the new root).
Now that we've seen how to enqueue, let's see how to dequeue. The first part is easy: as already mentioned, the item with the highest priority is at node 0. If we take it away, though, we break the binary tree. So, let's patch it up by moving the item at the rightmost end of the last layer in its place. With this simple move we have made the binary tree complete again, with the understanding that we've of course broken the heap property.
Enter the reverse operation to bubble-up, trickle-down. Look at the two children, if the item we've just moved is less than either or both of its children, swap it over with the larger child. Consider the item in its new place and perform the same operation. Continue doing this until the item is either greater than both its children or it has reached the bottom layer and has no children.
Trickle-down is more complicated than bubble-up because we have two children to consider (and, remember, every now and then, we'll only have one child to compare against). We also have to do two comparisons at every level: the two children against each other, and then the item against the larger child. To try and even up the balance and make trickle-down a little more efficient, what many people do is to just compare the two children and swap with the larger even though the parent item may be larger than both children. Once the item reaches the bottommost layer, we do a bubble-up operation to make sure the item's at the right level.
This sounds counter-intuitive (surely, we'd do roughly the same number of comparisons either way?), but in fact it can be much more efficient. Consider that the item appeared at the root to replace the item with the highest priority, but that it came from the bottommost level. That means that the item, in all probability, was one of the smallest items (in terms of priority) in the heap to begin with. In other words, it's likely that the item will find itself back on the bottommost level anyway. So, by doing the abbreviated trickle-down, we'll save some time in the long run.
Enough talk, let's implement. Since we're targeting .NET and the priority queue is a container, we should consider implementing one of the System.Collections interfaces. IEnumerable is a no-brainer, as is ICollection. IList is out: we are not allowing arbitrary inserts or removals form the priority queue (at least at this stage; we'll see about later on). So we should implement ICollection at most.
Since we're going to use TDD (Test-Driven Development) with NUnit, we should start off with a simple test case. The simplest one I can think of is to instantiate a priority queue and enqueue an item.
[Test] public TestEnqueueing() {
PriorityQueue pq = new PriorityQueue();
pq.Enqueue("item one", 12);
Assertion.AssertEquals(
"Enqueuing first item should set count to 1",
1, pq.Count);
}
What I'm aiming for is an Enqueue method that takes an item (the string in this case) and a priority (the 12).
Compile this and it fails (our red light). Time to write the actual code to make it (a) compile, and (b) pass the test.
using System;
using System.Collections;
namespace JMBucknall.Containers {
public class PriorityQueue : ICollection {
public PriorityQueue() {
}
public void Enqueue(object item, int priority) {
}
#region IEnumerable implementation
public IEnumerator GetEnumerator() {
throw new NotImplementedException();
}
#endregion
#region ICollection implementation
public int Count {
get {return 1;}
}
public void CopyTo(Array array, int index) {
throw new NotFiniteNumberException();
}
public object SyncRoot {
get {throw new NotFiniteNumberException();}
}
public bool IsSynchronized {
get {throw new NotFiniteNumberException();}
}
#endregion
}
}
Now, of course, I'm not saying that this is a good implementation of a priority queue (especially after the amount of description we've gone through), but it does pass the one and only test case we have so far. TDD tells us to implement the simplest code possible to pass a test, and this is pretty simple.
So, let's add another test: enqueuing another item.
[Test] public void TestEnqueueing() {
PriorityQueue pq = new PriorityQueue();
pq.Enqueue("item one", 12);
Assertion.AssertEquals(
"Enqueuing first item should set count to 1",
1, pq.Count);
pq.Enqueue("item two", 5);
Assertion.AssertEquals(
"Enqueuing second item should set count to 2",
2, pq.Count);
}
The second part of this test fails (the Count is wrong). Time to do some real work. Add a private member called count, increment it in Enqueue(), and return its value in Count's getter.
public class PriorityQueue : ICollection {
private int count;
public PriorityQueue() {
}
public void Enqueue(object item, int priority) {
count++;
}
...
#region ICollection implementation
public int Count {
get {return count;}
}
...
#endregion
}
Marvelous. Well, OK, it does leave a little to be desired, so let's write another test; this time to dequeue the item with the highest priority.
[Test] public void TestDequeueing() {
pq.Enqueue("item one", 12);
pq.Enqueue("item two", 5);
string s = (string) pq.Dequeue();
Assertion.AssertEquals(
"Dequeuing item should set count to 1",
1, pq.Count);
Assertion.AssertEquals(
"Dequeuing should retrieve highest priority item",
"item one", s);
}
This one fails, and fails good and proper. It's time to bite the bullet and implement the basic algorithm outlined above. Note that we have a couple of tests already which'll make sure we don't go too far astray.
The first thing we have to do is to devise a data structure that will combine an item with its priority. This is generally known as a tuple.
public struct HeapEntry {
private object item;
private int priority;
public HeapEntry(object item, int priority) {
this.item = item;
this.priority = priority;
}
public object Item {
get {return item;}
}
public int Priority {
get {return priority;}
}
}
I'm not worried about a test case for this simple class: it's going to be tested as part of the priority queue code.
Now we can flesh out the priority queue enough to make our tests work.
public class PriorityQueue : ICollection {
private int count;
private int capacity;
private HeapEntry[] heap;
public PriorityQueue() {
capacity = 15; // 15 is equal to 4 complete levels
heap = new HeapEntry[capacity];
}
public object Dequeue() {
object result = heap[0].Item;
count--;
trickleDown(0, heap[count]);
return result;
}
public void Enqueue(object item, int priority) {
count++;
bubbleUp(count - 1, new HeapEntry(item, priority));
}
private void bubbleUp(int index, HeapEntry he) {
int parent = (index - 1) / 2;
// note: (index > 0) means there is a parent
while ((index > 0) && (heap[parent].Priority < he.Priority)) {
heap[index] = heap[parent];
index = parent;
parent = (index - 1) / 2;
}
heap[index] = he;
}
private void trickleDown(int index, HeapEntry he) {
int child = (index * 2) + 1;
while (child < count) {
if (((child + 1) < count) &&
(heap[child].Priority < heap[child + 1].Priority)) {
child++;
}
heap[index] = heap[child];
index = child;
child = (index * 2) + 1;
}
bubbleUp(index, he);
}
...
}
Notice the code in trickleDown() that checks to see if there is a right child before comparing the left child to it.
The tests now run. so time to make it a little more interesting. Let's add a test to see what happens if we call Dequeue() on an empty queue. What I want to happen is an InvalidOperationException exception to be thrown.
[ExpectedException(typeof(InvalidOperationException))]
[Test] public void TestDequeueWithEmptyQueue() {
pq.Dequeue();
}
Of course, the test fails, so we add code to Dequeue() to make it succeed.
public object Dequeue() {
if (count == 0) {
throw new InvalidOperationException();
}
...
}
What next? Well, we're expecting the priority queue to grow if needed to accept more items. We set the initial capacity to 15 items in the constructor (it seemed like a good idea at the time), so now we should do some checking and some work in Enqueue() to make sure that it grows. First the test:
[Test] public void TestGrowingQueue() {
string s;
string expectedStr;
for (int i = 0; i < 15; i++) {
pq.Enqueue("item: " + i.ToString(), i * 2);
}
Assertion.AssertEquals(
"Enqueued 15 items, so there should be 15 there", 15, pq.Count);
pq.Enqueue("trigger", 15);
Assertion.AssertEquals(
"Enqueued another, so there should be 16 there", 16, pq.Count);
for (int i = 14; i > 7; i--) {
s = (string) pq.Dequeue();
expectedStr = "item: " + i.ToString();
Assertion.AssertEquals("Dequeueing problem", expectedStr, s);
}
s = (string) pq.Dequeue();
Assertion.AssertEquals("Dequeueing problem", "trigger", s);
for (int i = 7; i >= 0; i--) {
s = (string) pq.Dequeue();
expectedStr = "item: " + i.ToString();
Assertion.AssertEquals("Dequeueing problem", expectedStr, s);
}
}
This of course fails (we get an out-of-bounds exception thrown), so we write code to make it work:
public void Enqueue(object item, int priority) {
if (count == capacity)
growHeap();
count++;
bubbleUp(count - 1, new HeapEntry(item, priority));
}
private void growHeap() {
capacity = (capacity * 2) + 1;
HeapEntry[] newHeap = new HeapEntry[capacity];
System.Array.Copy(heap, 0, newHeap, 0, count);
heap = newHeap;
}
At this point, we have a functioning priority queue, but there still remain a few loose ends. For sure, we haven't implemented a lot of the methods from our interfaces, items like GetEnumerator() and the like. That will wait until next time when we'll finish off the priority queue class.
